こんにちは。サイちゃんです。

何をするにしても必要なのは、やっぱり仲間。
仲間がいるのと、いないのとでは、やはり全然違います。

一人が好きという人もいるだろうけど、仲間がいた方が絶対に良いです。

だから、勉強する仲間を作ることができる塾は、悪い場所ではないハズ。
ウチの塾は、そんな場所にしたいなと思っています。

そのためには、まずは、人が集まる場所にしないとね。

共感してくださる方。どんな形でもOKです！
お気軽にお問い合わせくだサイ！

こんにちは。サイちゃんです。

昨日、県立高校の倍率が発表されました。

これね、これ。
これねぇ、どうなん？

そんな感じの感想です。

今回変わった点と言えば、聞く話によると、今まで同一大学科でないと第2志望が書けなかったのが、今年から大学科が違っても第2志望を書けるようになったということ。
つまり、この辺で関係あるのは、今治北の普通科と商業科とで、横断して志願するできるようになったということ。

今までは、普通科が割れてても、商業科から転科合格することはあり得なかったですが、今年からはそれが起こるということです。逆もしかり。
それで、今回の倍率が、こんな感じ。

なるほど・・・という印象。

これね、良いの？本当にこんなことで。

そんな印象です。

詳しくは、こちらからご確認くだサイ。

こんにちは。サイちゃんです。

塾のHPをプチリニューアルしました。

えっ？！全然変わってない？
そう見えちゃう？

だから、プチリニューアルです。

見た目はあんまり変わっていないけれど、システムはかなり変わっています。
なので、上手く表示されないかもしれません。
ご迷惑おかけするかもしれませんが、何か見つけましたら、教えてくだサイ。

よろしくお願いします。

こんにちは。サイちゃんです。

今日ご紹介する記事はこちら

世の中の受験生や大人はFラン大の解像度が低いように思います。はっきり言いますが、皆さんが想像しているよりも大学としてのレベルを保てていないケースも存在するので、進学する際は本当にしっかり検討をしてほしいです。
だから進学は勧められない…。世の中のほとんどが知らないFラン大生の実態。大学全入時代だからこそ、進学の意味を考える。

Fラン大学に進学する意味はあるのか？という話。
何事においてもそうなのですが、何を目的にそうするのかということ。

一般的に大学は、勉強したり、研究したりするところです。
仮にそれを目的にするならば、Fラン大学でそれが出来るのかということをきちんと考えないといけないという話です。

就職に強いから大学にと考えているなら、Fランに限らず、それは懐疑的に捉えておくべきです。
地元の有力企業に就職したいなら、地元の実業高校の方が太いパイプがあるので、変な大学に行くよりは、地元の実業高校の方が楽に堅実な就職が出来るかもしれません。

勉強そっちのけで楽しいキャンパスライフを送りたいというなら、大学なんてどこでも良いのでしょうから、とりあえず大学に行くという選択肢はなくはないでしょう。

同じく、とりあえず、大学の卒業資格を持っておきたいというのであれば、Fラン大学だとしても行く価値はあるのかもしれません。大学の卒業資格を条件にしていることも少なくないです。

何事においても、目的です。それが一番大事。そこを見失うと、大切な時間とお金を無駄にすることになります。

ただ、記事にも書いてありますが、きちんと勉強さえしておけば、それなりの大学を選ぶことはできます。まずは、大学も学校なので、しっかり勉強してから行ってくだサイ。

ただ、中学校の学び直しをしたいのであれば、その辺の塾の方がよほど安上がりな気がします。
ところで、Fラン大学の近くに中高の学び直しの塾作れば儲かる時代がきそうで怖い。

こんにちは。サイちゃんです。

何でもそうですが、早めの行動って大事。

塾は、まだ良いかな？と思って先延ばしにしていると、大変なことになりますというお話です。

塾に慣れるのにも、勉強に慣れるにも時間がかかります。

始めるのが遅くなると、慣れた時には試合終了のホイッスルが鳴っているなんてことも少なくありません。

塾を意識した今が検討を始める瞬間です。
それは、通うかどうかではなく、どういった塾に通うかを検討することです。

意識をしているということは、何か困ったことがあるということです。
であれば、即行動です。

人間、なかなか重い腰が上がらないものですが、そこは頑張って腰を上げてくだサイ。
でないと、せっかく塾に通っても、効果が半減してしまいます。

こんにちは。サイちゃんです。

今日ご紹介する記事はこちら。

文部科学省は１３日午前、高校教育改革の基本方針を発表した。２０４０年に、公立高校の普通科で文系と理系の生徒の割合が同程度になるよう改革を進めることなどが柱となる。
公立高校の普通科、文系・理系の生徒の割合を同程度に…不足する理系人材育成へ文科省が基本方針

報道によりますと、今後、理系の人材不足を懸念した文科省が、普通科の理系の割合を文系と同数になるように目標を立てたとのこと。
ちなみに、今は、理系が3割弱、文系が半分弱、文理別けないが3割弱ということらしいです。

どのように目標を達成していくのか分かりませんが、そういうことらしいです。

例えば、理系は共通テスト１つ取っても、なんか不遇な扱いを受けています。

文系の人は、1日目で試験が終わるのに対して、理系は必ず2日必要とか。

これだけでも、気持ちがない人でないと受け付けられないような仕組みなっています。

そんな気持ちを作ることが出来るのか、よくわかりません。
その辺を改善していくのでしょうか？

まぁ、よくわかんないけど、理系が大切らしいです。
今のうちから、しっかり算数・数学、理科の勉強をしっかりしておいてくだサイ。

ということで、お問い合わせお待ちしています！

こんにちは。サイちゃんです。

内包関係が理解できない人が意外と多いようです。

これって、数学的なものの見方だから、数学って、大事だなと思う。
ちなみに、算数では、この領域に足を踏み入れないので、算数と数学は違う理由の1つになります。

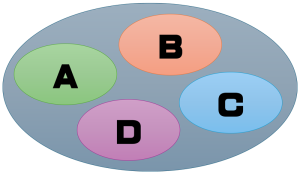
図のようなＡ、Ｂ、Ｃ、Ｄの意見があって、Aを否定する意見を言った場合を例にします。
このような意見を表明すると、必ずと言っていいほど、ＢやＣ、Ｄに関することを持ち出して、噛みついてくる人がいます。

あくまで、Ａについて否定的なことを言ったのであって、ＢやＣ、Ｄについては触れていません。
肯定も否定もしていません。

もしかすると、ＢもＣもＤも否定しているかもしれないし、Ａは否定するけど、Ｂ、Ｃ、Ｄについては肯定するかもしれません。
そんなことは読み取れないはずなのに、なぜか、勝手に関連付けて噛みついてくる人がいます。

ある事象のあるの部分だけを取り出しているのに、あたかも、全体を議論しているかのように読み取る。
日本語というよりも、数学を勉強してないんだろうな？と感じます。

ということで、数学はしっかり勉強してくだサイ。
特に、算数に毛の生えた計算はもちろんだけど、中2以降にで出てくる「証明」をしっかり勉強してくだサイ。

こんにちは。サイちゃんです。

やりたくないことは、やらなくて良いよという教育。
そんな世界があれば、過ごしやすいとは思うけど、本当にそうなのかな？

例えば、「来週までに、この部品作ってくれる？」と仕事をお願いした場合。
「いや、急にやる気が出なくなってさ、やりたくなかったんだよね」と、部品が作られなかったことが正当化されるということがまかり通るということ。

それで困るのは、仕事をお願いした人だからね。

そんな世界が過ごしやすい世界なのかな？

だから、やりたくないことでも、やらないといけないことは、やる練習をしないといけないと思う。
自分がやると決めたのなら、やり通さないとね。

勉強って、そういう練習をするのに丁度いいことだと思うよ。

やりたくないことも、やる気が出ないときも、パフォーマンスは下がるかもしれないけれど、やらないと終わらないから、しっかりやってくだサイ。

こんにちは。サイちゃんです。

辞書を引いていて、「大日本帝国憲法」が目に入った小学生。
「今日って、大日本帝国憲法ができた日だよね？」と。
小学生で、そんなことを言うなんて将来有望です。

とは言っても、今日は建国記念の日。
日本の誕生日とされている日です。
そして、初代天皇である神武天皇が即位した日と言われている日です。
されているというのは、古すぎてイマイチよくわからないらしいです。

でも、これは全部逆で、神武天皇が即位したと言われる2月11日を建国記念の日として、
また、その日を狙って大日本帝国憲法を発布したということらしいです。

色々渋滞して、情報過多な日ですが、神武天皇を中心に覚えると、覚えやすいかも？

皆さんも、日本の誕生日、お祝いしてくだサイ。

こんにちは。サイちゃんです。

どこの学校も、来週テスト発表、再来週テストのようです。
テスト期間中に3連休があるのは良いよね。

今年度最後のテストになります。
調査書に載る成績は学年のものだから、今回一発逆転できれば、もしかすると・・・？

早めに対策に取り組んで、気持ちよく今年度を終わらせてくだサイ。