こんにちは。サイちゃんです。

ちょっと話題になっているようです。

投稿で紹介された問題は、8cm辺の正方形に収まったアーモンド形の面積を求めるというもの。扇形の面積から三角形の面積を引き算し、それをさらに2倍するという、ひとつの公式を使ったでは解けない複合図形です。
「こんなの解けるわけない！」話題の〝アーモンド型〟面積問題、母も思わず検索した難問に共感殺到「大人でも無理」

この問題です。

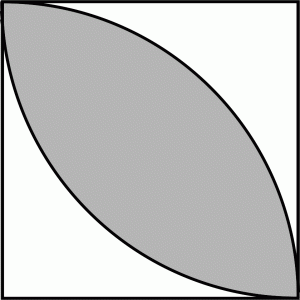
グレーに塗られたアーモンドの面積を求める問題。
塾長曰く、「アーモンド？ラグビーボールじゃないの？」と。
ハハっ

それはそれとして、
これは、扇形の面積を引いたり足したりしながら求めるんだけど、
円周率が3.14ならば、正方形の面積の57%になるらしいです。

この図形は、必ず相似になる図形なので、公式化しやすい図形ではあります。

で、この公式化に賛否両論。

見ていて感じたのは、
公式を使って楽をするという意味が大きく2種類あるということ。

1つは、全て理解した上で、公式を使うことで楽ができるという人。
もう1つは、思考停止で、正方形の面積に0.57かければ良いんでしょ？と何も考えずに公式を使う人。

前者の場合は、優秀な人なので何の問題もないですが、問題は後者の人。
思考停止で、こういう覚え方をしてしまうと、中学生になって、円周率がπになっても、
正方形の面積に0.57かけて解いてしまします。完全に詰んでます。応用が効かないにもほどがあります。

こういう子は、円周率がπに変わったから、その方法では解けないと説明しても、小学校の時は、これで出来たという成功体験からか、何度説明しようとしても、聞く耳を持たなかったりします。

この2種類を同一視して語ると、何やら歪なことになって、おかしなことになるんだろうなと思います。

優秀な人は、「何で公式化がダメなんだ！」と言うし、
思考停止している子達見てきた指導する立場の人は、公式化に疑問を持つことになります。

でも、とりあえず未来のことなんか関係なく、今、点を取らせたらいいんだろ？という指導者は、簡単に点を取らすことができるから推奨するだろうし。

この全体像が見えずに議論しているように見える人が、多すぎるなと感じました。

議論するときには、1歩引いて全体を見るようにしてくだサイ。