|
今回は、有効数字のお話。
英語ではmessential figureとか、significant digitsと言うそうです。
今の中学校の理科の教科書からは、有効数字の考え方が完全に削除されています。
しかし、なぜか、数学の教科書で触れられています。
これが、意味不明。
そろそろ、1年生が、有効数字がわからなくて、
パニックになっているころではないかと思い、解説してみます。
確率・統計の分野※は、数学というよりも、どちらかと言えば、理科に近い単元です。
一度、数学ということを忘れて、取り組んだ方が、理解しやすいかもしれません。
では、本題です。
ここに、1243gのお肉があります。

このお肉を、0.1kgまで量れるはかりに乗せると、1.2kgと表示されますよね?
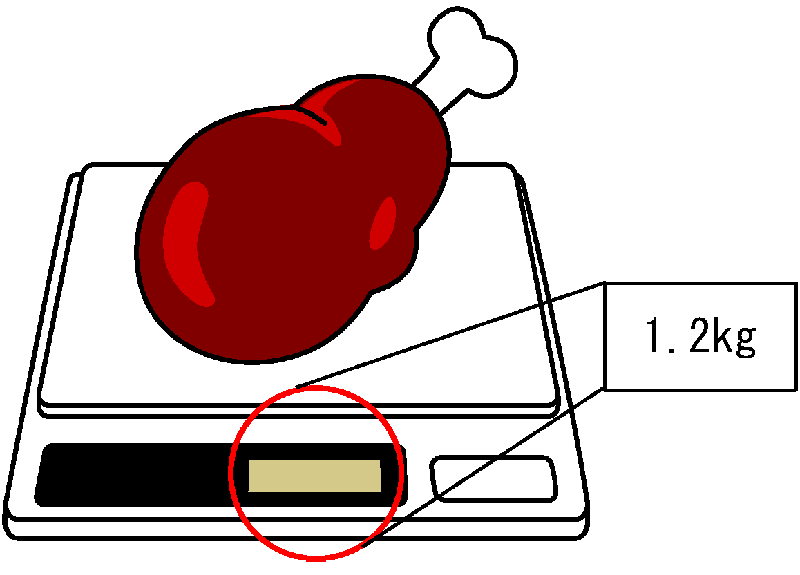
これをgに直すと、1200gになりますね?
でも、本当は、1243gあるのに、1200gと書いてしまうと、なんか違和感ありませんか?
本当は、1243gあるのに、はかりの性能で1200gと表示されてしまいます。
でも、1.2kgと表現すれば、なんとなく納得できますよね?
これが、有効数字です。
今回の場合は、1200の後ろの00は、信じられません。
ようは、0という数字に意味があるかないかが問題なのです。
そこで、信憑性のある、意味のある(信用できる)数字0と、
意味のない(信用できない)数字0を区別する方法を昔の人が考えました。
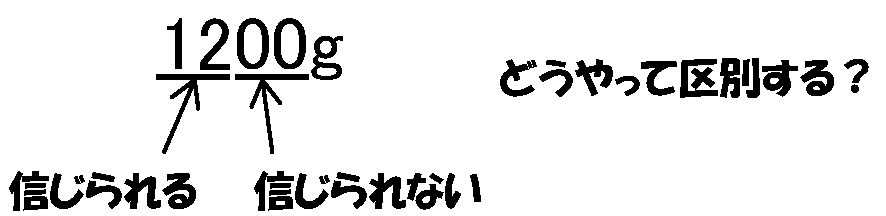
昔の人は、1.2×103 gと表すことにしました。
もし、10gまで量ることができるはかりでこの肉を量ると、1240gと表示されます。
そうすると、信じられる数字は、124の3ケタで、1の位の0は、信じられません。
でも、1240gと表すと、違和感ですね。
なので、1.24×103 gと表現します。
書かなければ、気にならないという訳です。
もちろん、1.24×1000と表しても良いんですが、「×1000・・・」の部分の0の数が増えると、
大変なことになるので、累乗を使って表します。
便利なのは、1.2×104、1.5×104、5.65×104、6.2×103、・・・
これらの数字の大きさを比べるとき、有効数字の桁数が変わっても、
どれが大きいか一目でわかることですね。
まず、比べるのは、累乗の指数。当たり前ですが、大きければ、大きいです。
それが等しければ、有効数字の1桁目、2桁目と順々に比べれば良いわけです。
一目で、大小を比べられるわけです。便利ですね。
※確率・統計の分野・・・1年生の資料、2年生の確率、3年生の標本調査の単元の総称
こちらもチェック
|